Program for array rotation

Question

Given an array of integers arr[ ] of size N and an integer, the task is to rotate the array elements to the left by d positions.

Examples:

Input: arr[ ] = {1,2, 3,4, 5,6, 7}, d = 2 Output: 3 4 5 6 7 1 2

Input: arr[ ] = {3,4, 5,6, 7,1, 2}, d=2 Output: 5 6 7 1 2 3 4

Approach 1 (Using temp array)

This problem can be solved using the idea: After rotating d positions to the left, the first d elements become the last d elements of the array

• First store the elements from index d to N-1 into the temp array.
• Then store the first d elements of the original array into the temp array.
• Copy back the elements of the temp array into the original array

Illustration

Suppose the give array is arr[ ] = [1,2, 3,4, 5,6, 7], d = 2.

First Step:     => Store the elements from 2nd index to the last.     => temp[ ] = [3,4, 5,6, 7]

Second Step:     => Now store the first 2 elements into the temp[ ] array.     => temp[ ] = [3,4, 5,6, 7,1, 2]

Third Steps:     => Copy the elements of the temp[ ] array into the original array.     => arr[ ] = temp[ ] So arr[ ] = [3,4, 5,6, 7,1, 2]

Follow the steps below to solve the given problem.

• Initialize a temporary array(temp[n]) of length same as the original array
• Initialize an integer(k) to keep a track of the current index
• Store the elements from the position d to n-1 in the temporary array
• Now, store 0 to d-1 elements of the original array in the temporary array
• Lastly, copy back the temporary array to the original array

Implementation

Below is the implementation of the above approach :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

function rotateArray(arr, n, d) {
    if (d < 0) {
        throw new Error("d must be greater than or equal to 0")
    }
    let newArr = new Array(n);
    let index = 0;
    for (let i = d; i < n; ++i) {
        newArr[index++] = arr[i];
    }

    for (let i = 0; i < d; ++i) {
        // Error
        // newArr[newArr.length] = arr[i];
        newArr[index++] = arr[i];
    }

    return newArr;
}

let arr = [1, 2, 3, 4, 5, 6, 7];
let newArr = rotateArray(arr, 7, 2);
for (const num of newArr) {
    process.stdout.write(num + ' ');
}
console.log()
newArr = rotateArray(arr, 7, 8);
for (const num of newArr) {
    process.stdout.write(num + ' ');
}

1
2

3 4 5 6 7 1 2
2 3 4 5 6 7 1

Time complexity: $O(N)$ Auxiliary Space: $O(N)$

Approach 2 (Rotate one by one)

This problem can be solved using the below idea:

• At each iteration, shift the elements by one position to the left circularly _{{ 循环地 }} (i.e., first element becomes the last).
• Perform this operation d times to rotate the elements to the left by d position.

Illustration

Let us take arr[ ] = [1,2, 3,4, 5,6, 7], d = 2.

First Step:         => Rotate to left by one position.         => arr[ ] = {2,3, 4,5, 6,7, 1}

Second Step:         => Rotate again to left by one position         => arr[ ] = {3,4, 5,6, 7,1, 2}

Rotation is done by 2 times. So the array becomes arr[ ] = {3,4, 5,6, 7,1, 2}

Follow the steps below to solve the given problem.

• Rotate the array to left by one position. For that do the following:
  • Store the first element of the array in a temporary variable.
  • Shift the rest of the elements in the original array by one place.
  • Update the last index of the array with the temporary variable.
• Repeat the above steps for the number of left rotations required.

Implementation

Below is the implementation of the above approach:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

function rotateArray(arr, n, d) {
    if (d < 0) {
        throw new Error('d must be greater than or equal to 0');
    }
    d = d % n;
    let count = 0;
    while (count < d) {
        let last = arr[0];
        for (let i = 0; i < n - 1; ++i) {
            arr[i] = arr[i + 1];
        }
        arr[n - 1] = last;
        ++count;
    }
    return arr;
}

let arr = [1, 2, 3, 4, 5, 6, 7];
let newArr = rotateArray(Array.from(arr), 7, 2);
for (const num of newArr) {
    process.stdout.write(num + ' ');
}
console.log()
newArr = rotateArray(Array.from(arr), 7, 8);
for (const num of newArr) {
    process.stdout.write(num + ' ');
}

1
2

3 4 5 6 7 1 2
2 3 4 5 6 7 1

Time Complexity: $O(N * d)$ Auxiliary Space: $O(1)$

Approach 3 (A Juggling Algorithm)

This is an extension of method 2.

Instead of moving one by one, divide the array into different sets where the number of sets is equal to the GCD of N and d (say X. So the elements which are X distance apart are part of a set) and rotate the elements within sets by 1 position to the left.

• Calculate the GCD between the length and the distance to be moved.
• The elements are only shifted within the sets.
• We start with temp = arr[0] and keep moving arr[I+d] to arr[I] and finally store temp at the right place.

Follow the below illustration for a better understanding

Illustration

Each steps looks like following:

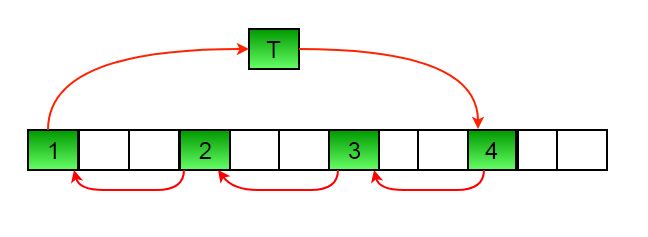
Let arr[ ] = {1,2, 3,4, 5,6, 7,8, 9,10,11,12} and d = 3

First step: => First set is {1,4, 7,10}. => Rotate this set by one position to the left. => This set becomes {4,7, 10,1} => Array arr[ ] = {4,2, 3,7, 5,6, 10,8, 9,1, 11,12}

Second step: => Second set is {2,5, 8,11}. => Rotate this set by one position to the left. => This set becomes {5,8, 11,2} => Array arr[ ] = {4,5, 3,7, 8,6, 10,11,9, 1,2, 12}

Third step: => Third set is {3,6, 9,12}. => Rotate this set by one position to the left. => This set becomes {6,9, 12,3} => Array arr[ ] = {4,5, 6,7, 8,9, 10,11,12,1, 2,3}

Follow the steps below to solve the given problem.

• Perform $d \bmod n$ in order to keep the value of d within the range of the array where d is the number of times the array is rotated and n is the size of the array.
• Calculate the GCD(n, d) to divide the array into sets.
• Run a for loop from 0 to the value obtained from GCD.
  • Store the value of arr[i] in a temporary variable (the value of i denotes the set number).
  • Run a while loop to update the values according to the set.
• After exiting the while loop assign the value of arr[j] as the value of the temporary variable (the value of j denotes the last element of the i-th set).

Implementation

Below is the implementation of the above approach :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

function gcd(a, b) {
    if (0 == b) {
        return a;
    } else {
        return gcd(b, a % b);
    }
}

function rotateArray(arr, n, d) {
    d = d % n;
    const count = gcd(n, d);
    for (let i = 0; i < count; ++i) {
        let tmp = arr[i];
        let j = i;
        while (1) {
            let k = j + d;
            if (k >= n) {
                k -= n;
            }
            if (i == k) {
                break;
            }
            arr[j] = arr[k];
            j = k;
        }
        arr[j] = tmp;
    }
    return arr;
}

let arr = [1, 2, 3, 4, 5, 6, 7];
let newArr = rotateArray(Array.from(arr), 7, 2);
for (const num of newArr) {
    process.stdout.write(num + ' ');
}
console.log()
newArr = rotateArray(Array.from(arr), 7, 5);
for (const num of newArr) {
    process.stdout.write(num + ' ');
}

1
2

3 4 5 6 7 1 2
6 7 1 2 3 4 5

Approach 4 (The Reversal Algorithm)

Here we will be discussing another method which uses the concept of reversing a part of array. The intuition behind the idea is mentioned below:

Intuition

If we observe closely, we can see that a group of array elements is changing its position. For example see the following array: arr[ ] = {1,2, 3,4, 5,6, 7} and d = 2. The rotated array is {3,4, 5,6, 7,1, 2}

The group having the first two elements is moving to the end of the array. This is like reversing the array.

• But the issue is that if we only reverse the array, it becomes {7,6, 5,4, 3,2, 1}.
• After rotation the elements in the chunks having the first 5 elements {7,6, 5,4, 3} and the last 2 elements {2,1} should be in the actual order as of the initial array [i.e., {3,4, 5,6, 7} and {1,2}]but here it gets reversed.
• So if those blocks are reversed again we get the desired rotated array.

So the sequence of operations is:

• Reverse the whole array
• Then reverse the last ‘d’ elements and
• Then reverse the first (N-d) elements.

As we are performing reverse operations it is also similar to the following sequence:

• Reverse the first ‘d’ elements
• Reverse last (N-d) elements
• Reverse the whole array.

Algorithm

The algorithm can be described with the help of the below pseudocode:

1
2
3
4
5
6
7
8
9

Algorithm reverse(arr, start, end):
  mid = (start + end) / 2
  loop from i = start to mid:
    swap (arr[i], arr[end-(mid-i+1)])

Algorithm rotate(arr, d, N):
  reverse(arr, 1, d) ;
  reverse(arr, d + 1, N);
  reverse(arr, 1, N);

Illustration

Follow the illustration _{{ 插图 }} below to for better understanding of the algorithm and intuition:

For example take the array arr[ ] = {1,2, 3,4, 5,6, 7} and d = 2.

The rotated array will look like:

1st Step: Consider the array as a combination of two blocks. One containing the first two elements and the other containing the remaining elements as shown above.

2nd Step: Now reverse the first d elements. It becomes as shown in the image

3rd Step: Now reverse the last (N-d) elements. It become as it is shown in the below image:

4th Step: Now the array is the exact reversed form of how it should be if left shifted d times. So reverse the whole array and you will get the required rotated array.

See that the array is now the same as the rotated array.

Implementation

Below is the implementation of the above approach:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

// reverse elements within the range of [left, right]
function reverse(arr, left, right) {
    for (let i = left, j = right; i < j; ++i, --j) {
        let tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

function rotateArray(arr, n, d) {
    if (d < 0) {
        throw new Error('d must be greater than or equal to 0');
    }
    d = d % n;
    if (0 === d) {
        return arr;
    }
    reverse(arr, 0, d - 1);
    reverse(arr, d, n - 1);
    reverse(arr, 0, n - 1);
    return arr;
}

let arr = [1, 2, 3, 4, 5, 6, 7];
let newArr = rotateArray(Array.from(arr), 7, 2);
for (const num of newArr) {
    process.stdout.write(num + ' ');
}
console.log()
newArr = rotateArray(Array.from(arr), 7, 5);
for (const num of newArr) {
    process.stdout.write(num + ' ');
}

1
2

3 4 5 6 7 1 2
6 7 1 2 3 4 5

Time Complexity: $O(N)$ Auxiliary Space: $O(1)$

Approach 5 (Block swap)

Algorithm

Initialize A = arr[0..d-1] and B = arr[d..n-1], Do following until size of A is equal to size of B

• If A is shorter, divide B into Bl and Br such that Br is of same length as A. Swap A and Br to change ABlBr into BrBlA. Now A is at its final place, so recur on pieces of B.
• If A is longer, divide A into Al and Ar such that Al is of same length as B Swap Al and B to change AlArB into BArAl. Now B is at its final place, so recur on pieces of A.
• Finally when A and B are of equal size, block swap them.

Below is the implementation of the above approach:

Time Complexity: $O(N)$ Auxiliary Space: $O(1)$

References

• https://www.geeksforgeeks.org/array-rotation/
• https://www.faceprep.in/c-plus-plus/juggling-algorithm-for-array-rotation/
• https://www.geeksforgeeks.org/program-for-array-rotation-continued-reversal-algorithm/