221. 最大正方形

题目描述

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

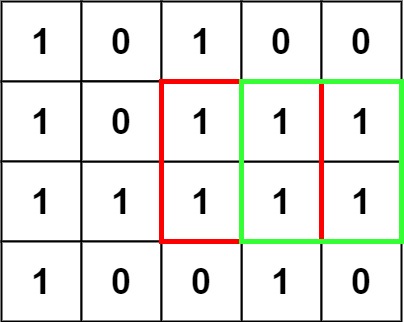
输入：matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出：4

示例 2：

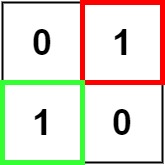
输入：matrix = [[“0”,“1”],[“1”,“0”]]
输出：1

示例 3：

输入：matrix = [[“0”]]
输出：0

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] 为 '0' 或 '1'

解法一：预处理 + 单调栈

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


func maximalSquare(matrix [][]byte) int {
    h, w := len(matrix), len(matrix[0])
    left := make([][]int, h+1)
    for i := 0; i <= h; i++ {
        left[i] = make([]int, w)
    }
    for i := 0; i < h; i++ {
        for j := 0; j < w; j++ {
            if j > 0 {
                left[i][j] = left[i][j-1]
            }
            if matrix[i][j] == '0' {
                left[i][j] = 0
            } else {
                left[i][j] += 1
            }
        }
    }
    width := 0
    stack := make([]int, 0, h+1)
    for j := 0; j < w; j++ {
        stack = append(stack, -1)
        for i := 0; i <= h; i++ {
            for stack[len(stack)-1] != -1 && left[stack[len(stack)-1]][j] > left[i][j] {
                h := left[stack[len(stack)-1]][j]
                stack = stack[:len(stack)-1]
                w := i - stack[len(stack)-1] - 1
                if w >= h && h > width {
                    width = h
                }
            }
            stack = append(stack, i)
        }
        stack = stack[:0]
    }
    return width * width
}

解法二：动态规划

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


func min(nums ...int) int {
    res := nums[0]
    for _, num := range nums {
        if num < res {
            res = num
        }
    }
    return res
}

func maximalSquare(matrix [][]byte) int {
    h, w := len(matrix), len(matrix[0])
    dp := make([][]int, h)
    for i := 0; i < h; i++ {
        dp[i] = make([]int, w)
    }
    width := 0
    for i := 0; i < h; i++ {
        for j := 0; j < w; j++ {
            if i == 0 || j == 0 {
                dp[i][j] = int(matrix[i][j] - '0')
            } else if matrix[i][j] == '1' {
                dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
            }
            if dp[i][j] > width {
                width = dp[i][j]
            }
        }
    }
    return width * width
}