329. 矩阵中的最长递增路径

题目描述

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。你不能在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 2³¹ - 1

解法一：DFS + 记忆化搜索

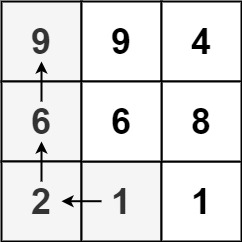
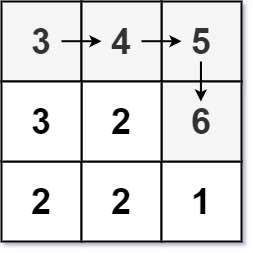
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49


func max(nums ...int) int {
    res := nums[0]
    for _, num := range nums {
        if num > res {
            res = num
        }
    }
    return res
}

func longestIncreasingPath(matrix [][]int) int {
    h, w := len(matrix), len(matrix[0])
    dirs := [][2]int{{1, 0}, {0, 1}, {-1, 0}, {0, -1}}
    m := make(map[int][]int)
    for i := 0; i < h; i++ {
        for j := 0; j < w; j++ {
            for _, dir := range dirs {
                ni, nj := i+dir[0], j+dir[1]
                if 0 <= ni && ni < h && 0 <= nj && nj < w {
                    a := i*w + j
                    b := ni*w + nj
                    if matrix[i][j] < matrix[ni][nj] {
                        m[a] = append(m[a], b)
                    } else if matrix[ni][nj] < matrix[i][j] {
                        m[b] = append(m[b], a)
                    }
                }
            }
        }
    }
    record := make([]int, h*w)
    ans := 0
    var dfs func(idx int) int
    // dfs[i] 表示以 i 为起点的最长递增路径
    dfs = func(idx int) int {
        if record[idx] > 0 {
            return record[idx]
        }
        for _, nxt := range m[idx] {
            record[idx] = max(record[idx], dfs(nxt))
        }
        record[idx] += 1
        return record[idx]
    }
    for i := 0; i < h*w; i++ {
        ans = max(dfs(i), ans)
    }
    return ans
}