654. 最大二叉树

题目描述

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

示例 1：

输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：

- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

解法一：纯递归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


func constructMaximumBinaryTree(nums []int) *TreeNode {
    if len(nums) == 0 {
        return nil
    }
    best := 0
    for i, num := range nums {
        if num > nums[best] {
            best = i
        }
    }
    return &TreeNode{
        nums[best],
        constructMaximumBinaryTree(nums[:best]),
        constructMaximumBinaryTree(nums[best+1:])
    }
}

解法二：线段树 + 递归

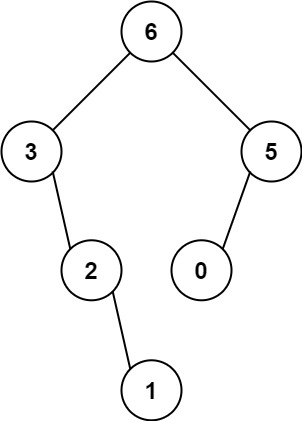
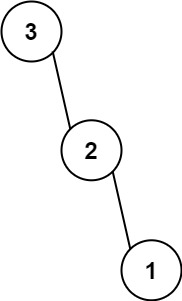
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83


type segmentTree struct {
    origin []int
    res    []int
}

func NewSegmentTree(arr []int) *segmentTree {
    ret := &segmentTree{origin: arr, res: make([]int, 4*len(arr))}
    ret.Build()
    return ret
}

func (this *segmentTree) Build() {
    var _build func(idx, l, r int) int
    _build = func(idx, l, r int) int {
        if l == r {
            this.res[idx] = this.origin[l]
        } else {
            mid := l + (r-l)/2
            leftMax := _build(2*idx, l, mid)
            rightMax := _build(2*idx+1, mid+1, r)
            this.res[idx] = max(leftMax, rightMax)
        }
        return this.res[idx]
    }
    _build(1, 0, len(this.origin)-1)
}

func (this *segmentTree) GetMax(tl, tr int) int {
    var _getMax func(idx, l, r, tl, tr int) int
    // [l...r] 是 segmentTree 中的 segment
    // [tl...tr]是目标 segment
    _getMax = func(idx, l, r, tl, tr int) int {
        if l > r {
            return math.MinInt32
        } else if l == tl && r == tr {
            return this.res[idx]
        } else {
            mid := l + (r-l)/2
            if tr <= mid {
                return _getMax(2*idx, l, mid, tl, tr)
            } else if tl >= mid+1 {
                return _getMax(2*idx+1, mid+1, r, tl, tr)
            } else {
                leftMax := _getMax(2*idx, l, mid, tl, mid)
                rightMax := _getMax(2*idx+1, mid+1, r, mid+1, tr)
                return max(leftMax, rightMax)
            }
        }
    }
    return _getMax(1, 0, len(this.origin)-1, tl, tr)
}

func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

func constructMaximumBinaryTree(nums []int) *TreeNode {
    sTree := NewSegmentTree(nums)
    record := make(map[int]int)
    for v, k := range nums {
        record[k] = v
    }

    var build func(l, r int) *TreeNode
    build = func(l, r int) *TreeNode {
        if l == r {
            return &TreeNode{Val: nums[l]}
        } else if l > r {
            return nil
        } else {
            maxNum := sTree.GetMax(l, r)
            idxOfMax := record[maxNum]
            root := &TreeNode{Val: maxNum}
            root.Left = build(l, idxOfMax-1)
            root.Right = build(idxOfMax+1, r)
            return root
        }
    }
    return build(0, len(nums)-1)
}