931. 下降路径最小和

题目描述

给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

示例 1：

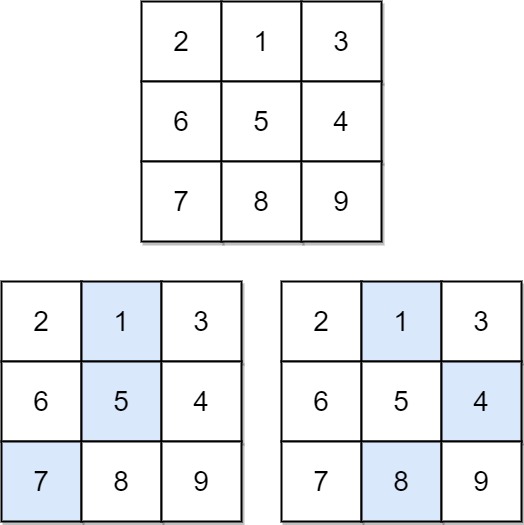
输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：如图所示，为和最小的两条下降路径

示例 2：

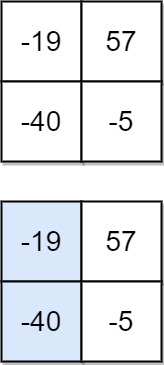
输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：如图所示，为和最小的下降路径

提示：

n == matrix.length == matrix[i].length
1 <= n <= 100
-100 <= matrix[i][j] <= 100

解法一：动态规划

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


func minFallingPathSum(matrix [][]int) int {
    h, w := len(matrix), len(matrix[0])
    dp := make([][]int, h)
    for i := 0; i < h; i++ {
        dp[i] = make([]int, w)
        for j := 0; j < w; j++ {
            dp[i][j] = math.MaxInt32
        }
    }
    for j := 0; j < w; j++ {
        dp[0][j] = matrix[0][j]
    }
    dirs := [][2]int{{-1, -1}, {-1, 1}, {-1, 0}}
    for i := 1; i < h; i++ {
        for j := 0; j < w; j++ {
            for _, dir := range dirs {
                prevI, prevJ := i+dir[0], j+dir[1]
                if prevI >= 0 && prevJ >= 0 && prevJ < w {
                    if dp[i][j] > dp[prevI][prevJ]+matrix[i][j] {
                        dp[i][j] = dp[prevI][prevJ] + matrix[i][j]
                    }
                }
            }
        }
    }

    ans := math.MaxInt32
    for j := 0; j < w; j++ {
        if ans > dp[h-1][j] {
            ans = dp[h-1][j]
        }
    }
    return ans
}