题目描述
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
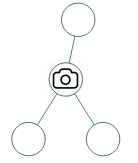
- 输入:[0,0,null,0,0]
- 输出:1
- 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
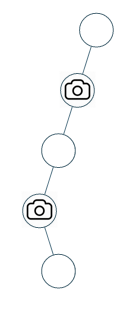
- 输入:[0,0,null,0,null,0,null,null,0]
- 输出:2
- 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
解法一:贪心
解题思路
一下解题思路来自 代码随想录 的思路,原文地址:968. 监控二叉树
这道题目其实不是那么好理解的,题目举的示例不是很典型,会误以为摄像头必须要放在中间,其实放哪里都可以只要覆盖了就行。
这道题目难在两点:
- 需要确定遍历方式
- 需要状态转移的方程
我们之前做动态规划的时候,只要最难的地方在于确定状态转移方程,至于遍历方式无非就是在数组或者二维数组上。
本题并不是动态规划,其本质是贪心,但我们要确定状态转移方式,而且要在树上进行推导,所以难度就上来了,一些同学知道这道题目难,但其实说不上难点究竟在哪。
确定遍历方式
首先先确定遍历方式,才能确定转移方程,那么该如何遍历呢?
在安排选择摄像头的位置的时候,我们要从底向上进行推导,因为尽量让叶子节点的父节点安装摄像头,这样摄像头的数量才是最少的 ,这也是本道贪心的原理所在!
如何从低向上推导呢?
就是后序遍历也就是左右中的顺序,这样就可以从下到上进行推导了。
后序遍历代码如下:
|
|
注意在以上代码中我们取了左孩子的返回值,右孩子的返回值,即 left 和 right, 以后推导中间节点的状态
确定状态转移的方程
确定了遍历顺序,再看看这个状态应该如何转移,先来看看每个节点可能有几种状态:
可以说有如下三种:
- 该节点无覆盖
- 本节点有摄像头
- 本节点有覆盖
我们分别有三个数字来表示:
- 0:该节点无覆盖
- 1:本节点有摄像头
- 2:本节点有覆盖
大家应该找不出第四个节点的状态了。
一些同学可能会想有没有第四种状态:本节点无摄像头,其实无摄像头就是无覆盖或者有覆盖的状态,所以一共还是三个状态。
那么问题来了,空节点究竟是哪一种状态呢? 空节点表示无覆盖? 表示有摄像头?还是有覆盖呢?
回归本质,为了让摄像头数量最少,我们要尽量让叶子节点的父节点安装摄像头,这样才能摄像头的数量最少。
那么空节点不能是无覆盖的状态,这样叶子节点就可以放摄像头了,空节点也不能是有摄像头的状态,这样叶子节点的父节点就没有必要放摄像头了,而是可以把摄像头放在叶子节点的爷爷节点上。所以空节点的状态只能是有覆盖,这样就可以在叶子节点的父节点放摄像头了。
接下来就是递推关系。
那么递归的终止条件应该是遇到了空节点,此时应该返回 2(有覆盖),原因上面已经解释过了。
代码如下:
|
|
递归的函数,以及终止条件已经确定了,再来看单层逻辑处理。
主要有如下四类情况:
-
情况 1:左右节点都有覆盖
左孩子有覆盖,右孩子有覆盖,那么此时中间节点应该就是无覆盖的状态了。
如图:
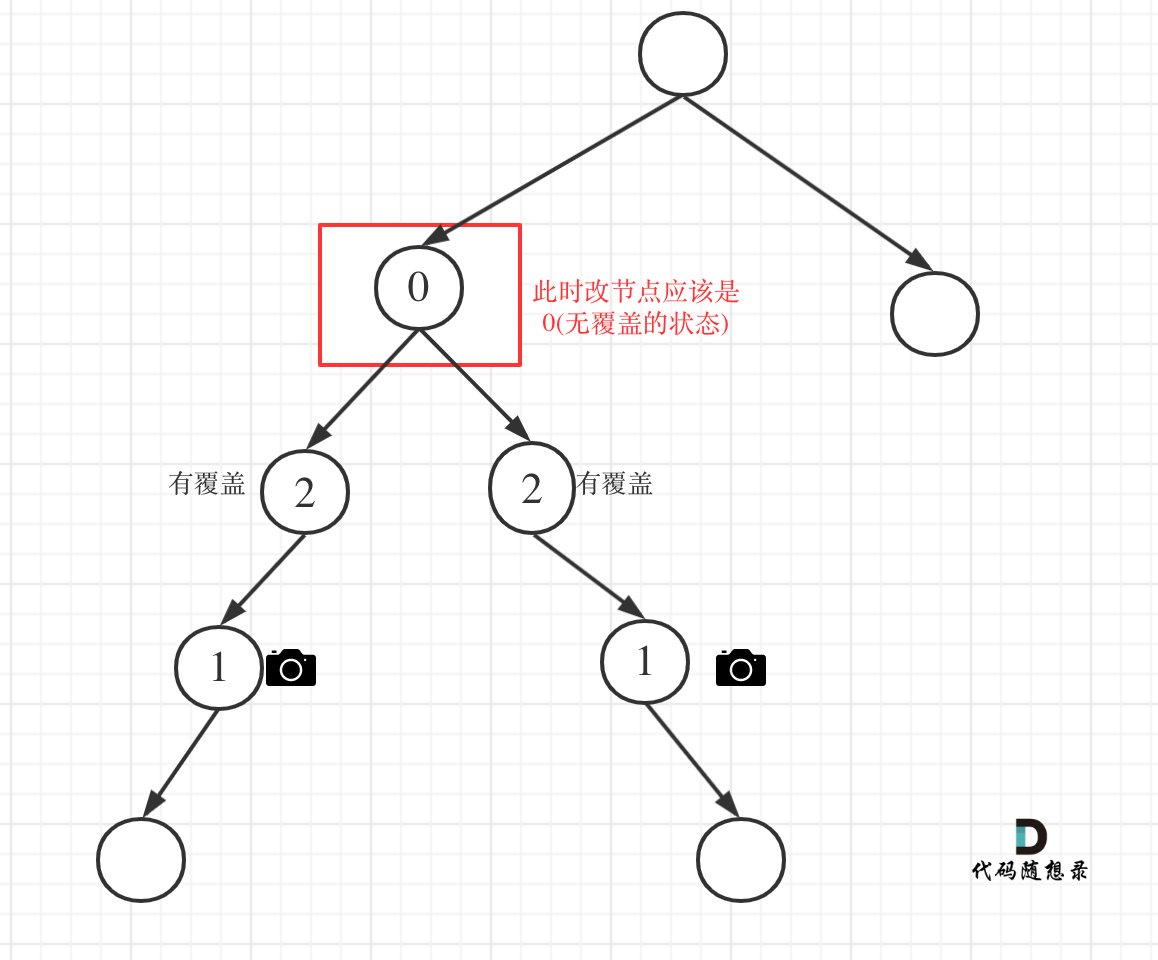
代码如下:
1 2// 左右节点都有覆盖 if (left == 2 && right == 2) return 0; -
情况 2:左右节点至少有一个无覆盖的情况
如果是以下情况,则中间节点(父节点)应该放摄像头:
left == 0 && right == 0左右节点无覆盖left == 1 && right == 0左节点有摄像头,右节点无覆盖left == 0 && right == 1左节点有无覆盖,右节点摄像头left == 0 && right == 2左节点无覆盖,右节点覆盖left == 2 && right == 0左节点覆盖,右节点无覆盖这个不难理解,毕竟有一个孩子没有覆盖,父节点就应该放摄像头。
此时摄像头的数量要加一,并且
return 1,代表中间节点放摄像头。代码如下:
1 2 3 4if (left == 0 || right == 0) { result++; return 1; } -
情况 3:左右节点至少有一个有摄像头
如果是以下情况,其实就是左右孩子节点有一个有摄像头了,那么其父节点就应该是 2(覆盖的状态)
- 左节点有摄像头,右节点有覆盖:
left == 1 && right == 2 - 左节点有覆盖,右节点有摄像头:
left == 2 && right == 1 - 左右节点都有摄像头:
left == 1 && right == 1
代码如下:
1if (left == 1 || right == 1) return 2;从这个代码中,可以看出,如果
left == 1,right == 0怎么办?其实这种条件在情况 2 中已经判断过了,如图: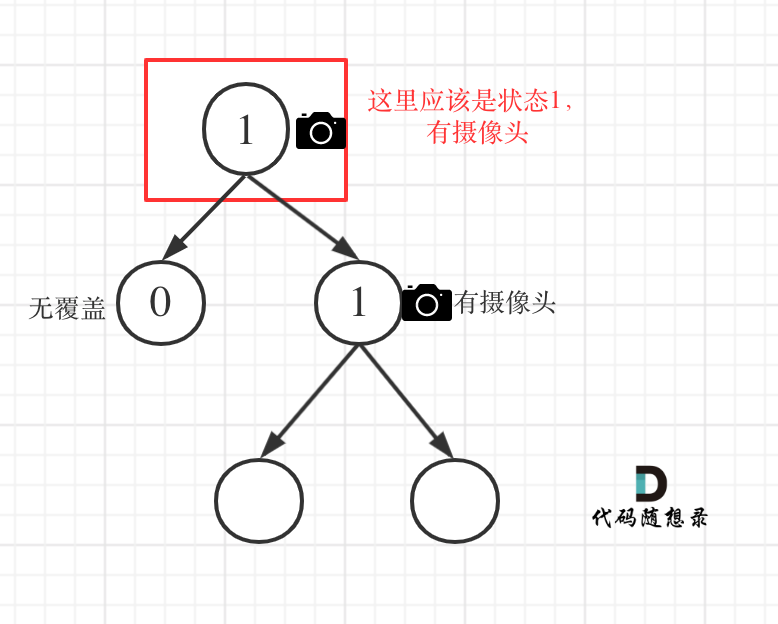
- 左节点有摄像头,右节点有覆盖:
-
情况 4:头结点没有覆盖
以上都处理完了,递归结束之后,可能头结点 还有一个无覆盖的情况,如图:
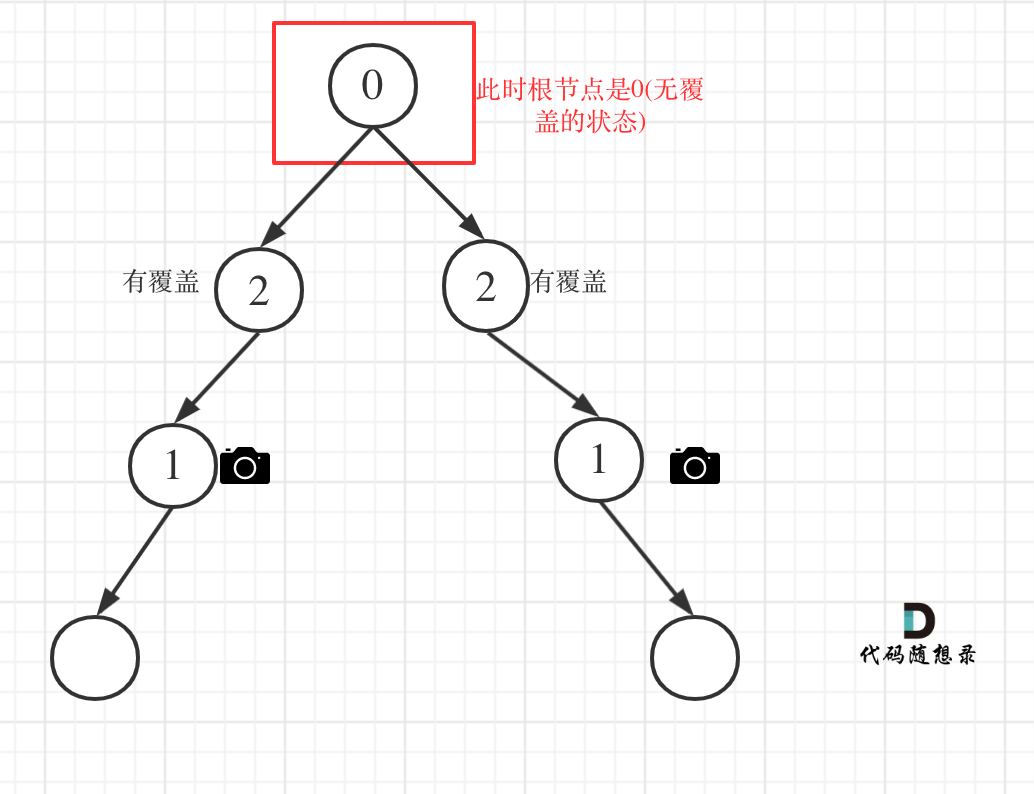
所以递归结束之后,还要判断根节点,如果没有覆盖,
result++
最终代码
最终的代码如下:
|
|
