1254. 统计封闭岛屿的数目

题目描述

二维矩阵 grid 由 0 （土地）和 1 （水）组成。岛是由最大的 4 个方向连通的 0 组成的群，封闭岛是一个 完全 由 1 包围（左、上、右、下）的岛。

请返回 封闭岛屿 的数目。

示例 1：

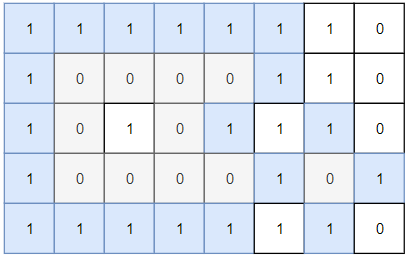
输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
输出：2
解释：灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。

示例 2：

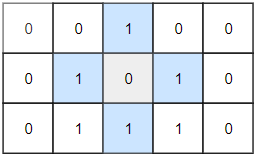
输入：grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
输出：1

示例 3：

输入：

输入：grid = [[1,1,1,1,1,1,1],
             [1,0,0,0,0,0,1],
             [1,0,1,1,1,0,1],
             [1,0,1,0,1,0,1],
             [1,0,1,1,1,0,1],
             [1,0,0,0,0,0,1],
             [1,1,1,1,1,1,1]]

输出：2

提示：

1 <= grid.length, grid[0].length <= 100
0 <= grid[i][j] <=1

解法一：BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35


func closedIsland(grid [][]int) int {
    m, n := len(grid), len(grid[0])
    dirs := [][2]int{{1, 0}, {0, 1}, {-1, 0}, {0, -1}}
    ans := 0
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] == 0 {
                closed := true
                var queue [][2]int
                queue = append(queue, [2]int{i, j})
                grid[i][j] = 1
                for len(queue) > 0 {
                    cur := queue[0]
                    queue = queue[1:]
                    x, y := cur[0], cur[1]
                    if x == 0 || x == m-1 || y == 0 || y == n-1 {
                        closed = false
                    }
                    for _, delta := range dirs {
                        nx, ny := x+delta[0], y+delta[1]
                        if nx < 0 || nx >= m || ny < 0 || ny >= n || grid[nx][ny] == 1 {
                            continue
                        }
                        grid[nx][ny] = 1
                        queue = append(queue, [2]int{nx, ny})
                    }
                }
                if closed {
                    ans++
                }
            }
        }
    }
    return ans
}

解法二：DFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


func closedIsland(grid [][]int) int {
    m, n := len(grid), len(grid[0])
    var dfs func(i, j int) bool
    dfs = func(i, j int) bool {
        if i < 0 || j < 0 || i >= m || j >= n {
            return false
        }
        if grid[i][j] != 0 {
            return true
        }
        grid[i][j] = 1
        a := dfs(i+1, j)
        b := dfs(i-1, j)
        c := dfs(i, j+1)
        d := dfs(i, j-1)
        return a && b && c && d
        // 注意：不可以使用如下一行代码替换上面 5 行代码
        // return dfs(i+1, j) && dfs(i-1, j) && dfs(i, j+1) && dfs(i, j-1)
    }

    ans := 0
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] == 0 && dfs(i, j) {
                ans++
            }
        }
    }
    return ans
}