1388. 3n 块披萨

题目描述

给你一个披萨，它由 3n 块不同大小的部分组成，现在你和你的朋友们需要按照如下规则来分披萨：

你挑选任意一块披萨。
Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
重复上述过程直到没有披萨剩下。

每一块披萨的大小按顺时针方向由循环数组 slices 表示。

请你返回你可以获得的披萨大小总和的最大值。

示例 1：

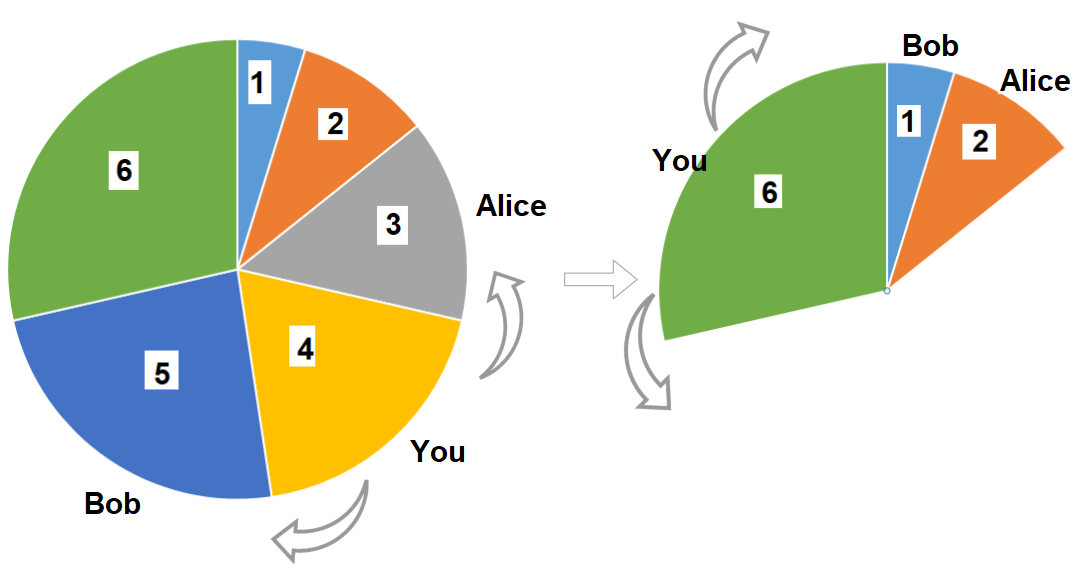
输入：slices = [1,2,3,4,5,6]
输出：10
解释：选择大小为 4 的披萨，Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨，Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。

示例 2：

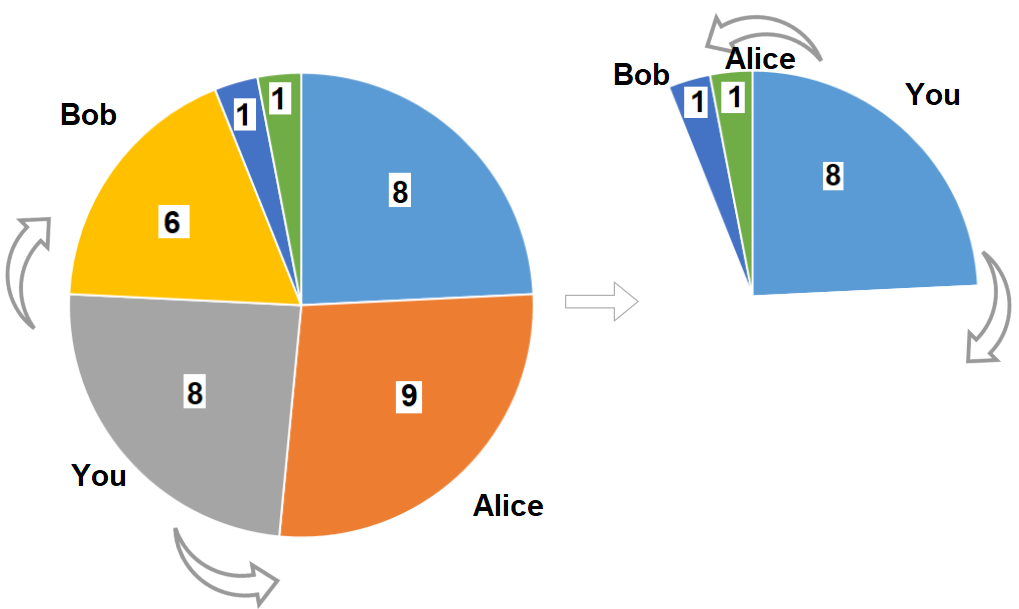
输入：slices = [8,9,8,6,1,1]
输出：16
解释：两轮都选大小为 8 的披萨。如果你选择大小为 9 的披萨，你的朋友们就会选择大小为 8 的披萨，这种情况下你的总和不是最大的。

提示：

1 <= slices.length <= 500
slices.length % 3 == 0
1 <= slices[i] <= 1000

解法一：动态规划

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


func max(nums ...int) int {
    res := nums[0]
    for _, num := range nums {
        if num > res {
            res = num
        }
    }
    return res
}

func maxSizeSlices(slices []int) int {
    M := len(slices) / 3
    var calc func(arr []int) int
    calc = func(arr []int) int {
        N := len(arr)
        // dp[i][j] 表示在前 i 个数中选择了 j 个不相邻的数的最大和
        dp := make([][]int, N)
        for i := 0; i < N; i++ {
            dp[i] = make([]int, M+1)
        }
        dp[0][1], dp[1][1] = arr[0], max(arr[0], arr[1])
        for j := 2; j <= M; j++ {
            dp[0][j], dp[1][j] = math.MinInt32, math.MinInt32
        }
        for i := 2; i < N; i++ {
            for j := 1; j <= M; j++ {
                dp[i][j] = max(dp[i-2][j-1]+arr[i], dp[i-1][j])
            }
        }
        return dp[N-1][M]
    }
    return max(calc(slices[1:]), calc(slices[:len(slices)-1]))
}