1444. 切披萨的方案数

题目描述

给你一个 rows x cols 大小的矩形披萨和一个整数 k ，矩形包含两种字符： 'A' （表示苹果）和 '.' （表示空白格子）。你需要切披萨 k-1 次，得到 k 块披萨并送给别人。

切披萨的每一刀，先要选择是向垂直还是水平方向切，再在矩形的边界上选一个切的位置，将披萨一分为二。如果垂直地切披萨，那么需要把左边的部分送给一个人，如果水平地切，那么需要把上面的部分送给一个人。在切完最后一刀后，需要把剩下来的一块送给最后一个人。

请你返回确保每一块披萨包含至少一个苹果的切披萨方案数。由于答案可能是个很大的数字，请你返回它对 10^9 + 7 取余的结果。

示例 1：

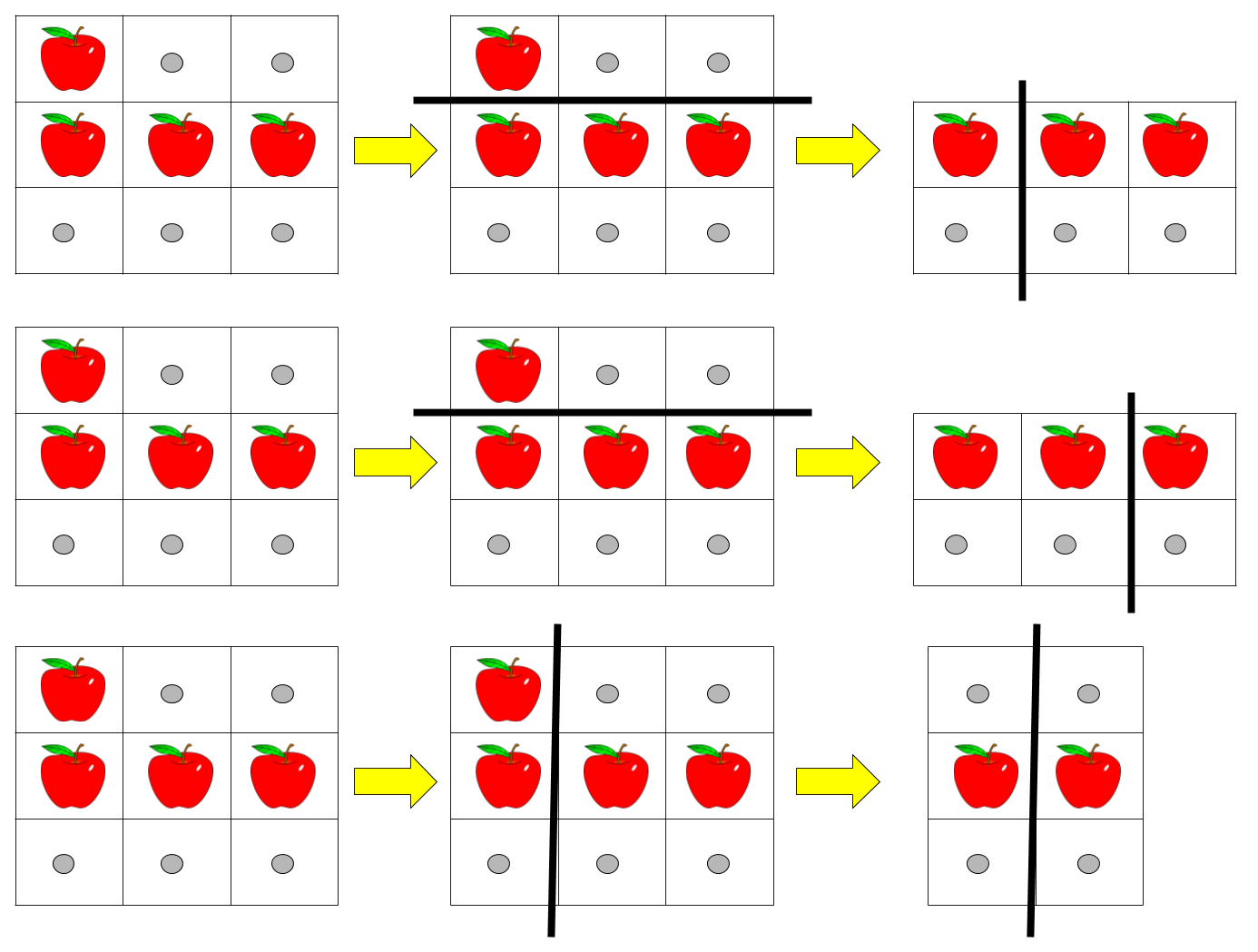
输入：pizza = [“A..”,“AAA”,"…"], k = 3
输出：3
解释：上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。

示例 2：

输入：pizza = [“A..”,“AA.”,"…"], k = 3
输出：1

示例 3：

输入：pizza = [“A..”,“A..”,"…"], k = 1
输出：1

提示：

1 <= rows, cols <= 50
rows == pizza.length
cols == pizza[i].length
1 <= k <= 10
pizza 只包含字符 'A' 和 '.' 。

解法一：动态规划

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47


func ways(pizza []string, k int) int {
    h, w := len(pizza), len(pizza[0])
    applies := make([][]int, h+1)
    for i := 0; i <= h; i++ {
        applies[i] = make([]int, w+1)
    }
    dp := make([][][]int, k+1)
    for i := 0; i <= k; i++ {
        dp[i] = make([][]int, h)
        for j := 0; j < h; j++ {
            dp[i][j] = make([]int, w)
        }
    }
    for i := h - 1; i >= 0; i-- {
        for j := w - 1; j >= 0; j-- {
            if pizza[i][j] == 'A' {
                applies[i][j] = 1
            }
            applies[i][j] += applies[i+1][j] + applies[i][j+1] - applies[i+1][j+1]
            if applies[i][j] >= 1 {
                dp[1][i][j] = 1
            }
        }
    }

    const MOD = int(1e9 + 7)
    for tk := 2; tk <= k; tk++ {
        for i := 0; i < h; i++ {
            for j := 0; j < w; j++ {
                for ti := i + 1; ti < h; ti++ {
                    // 根据题目要求，切一刀将披萨一分为二，每块披萨上都有苹果，
                    // 所以大披萨的苹果数量，要严格大于小披萨苹果数量，
                    // 小披萨的苹果数量，要严格大于零。
                    if applies[i][j] > applies[ti][j] && applies[ti][j] > 0 {
                        dp[tk][i][j] = (dp[tk][i][j] + dp[tk-1][ti][j]) % MOD
                    }
                }
                for tj := j + 1; tj < w; tj++ {
                    if applies[i][j] > applies[i][tj] && applies[i][tj] > 0 {
                        dp[tk][i][j] = (dp[tk][i][j] + dp[tk-1][i][tj]) % MOD
                    }
                }
            }
        }
    }
    return dp[k][0][0]
}