题目描述
给你两组点,其中第一组中有 size1 个点,第二组中有 size2 个点,且 size1 >= size2 。
任意两点间的连接成本 cost 由大小为 size1 x size2 矩阵给出,其中 cost[i][j] 是第一组中的点 i 和第二组中的点 j 的连接成本。如果两个组中的每个点都与另一组中的一个或多个点连接,则称这两组点是连通的。换言之,第一组中的每个点必须至少与第二组中的一个点连接,且第二组中的每个点必须至少与第一组中的一个点连接。
返回连通两组点所需的最小成本。
示例 1:
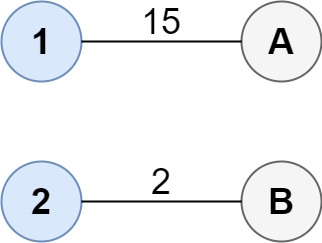
- 输入:cost = [[15, 96], [36, 2]]
- 输出:17
- 解释:连通两组点的最佳方法是:
示例 2:
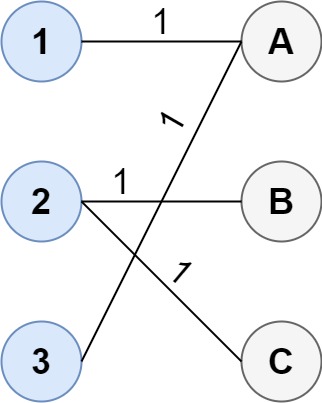
- 输入:cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
- 输出:4
- 解释:连通两组点的最佳方法是:
- 1–A
- 2–B
- 2–C
- 3–A
- 最小成本为 4 。请注意,虽然有多个点连接到第一组中的点 2 和第二组中的点 A ,但由于题目并不限制连接点的数目,所以只需要关心最低总成本。
示例 3:
- 输入:cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
- 输出:10
提示:
- size1 == cost.length
- size2 == cost[i].length
- 1 <= size1, size2 <= 12
- size1 >= size2
0 <= cost[i][j] <= 100
解法一:状态压缩 + 动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
func min(nums ...int) int {
res := nums[0]
for _, val := range nums {
if val < res {
res = val
}
}
return res
}
func connectTwoGroups(cost [][]int) int {
size1, size2 := len(cost), len(cost[0])
w := 1 << size2
dp := make([][]int, size1+1)
for i := 0; i <= size1; i++ {
dp[i] = make([]int, w)
for j := 0; j < w; j++ {
dp[i][j] = math.MaxInt32 / 2
}
}
dp[0][0] = 0
for i := 1; i <= size1; i++ {
for j := 1; j < w; j++ {
for k := 0; k < size2; k++ {
if j&(1<<k) == 0 {
continue
}
dp[i][j] = min(dp[i][j], dp[i][j^(1<<k)]+cost[i-1][k])
dp[i][j] = min(dp[i][j], dp[i-1][j]+cost[i-1][k])
dp[i][j] = min(dp[i][j], dp[i-1][j^(1<<k)]+cost[i-1][k])
}
}
}
return dp[size1][w-1]
}
|


