1631. 最小体力消耗路径

题目描述

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往上，下，左，右四个方向之一移动，你想要找到耗费体力最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

示例 1：

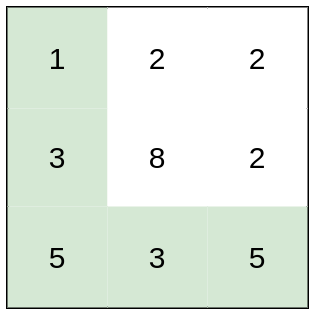
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

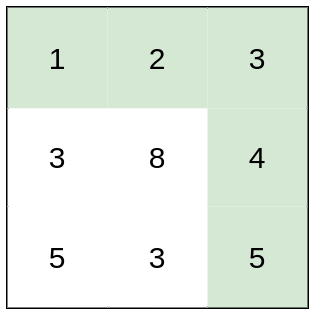
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

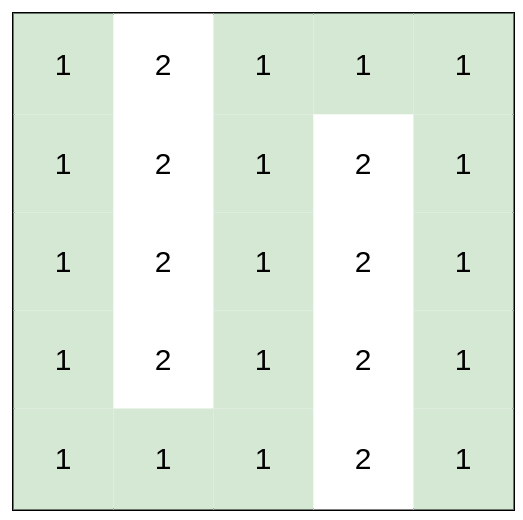
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10⁶

解法一：BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


func abs(num int) int {
    if num < 0 {
        return -num
    }
    return num
}

func minimumEffortPath(heights [][]int) int {
    h, w := len(heights), len(heights[0])
    left, right := 0, int(1e6-1)
    dirs := [][2]int{{1, 0}, {0, 1}, {-1, 0}, {0, -1}}
    for left < right {
        mid := left + (right-left)/2
        var queue [][2]int
        seen := make(map[int]bool)
        queue = append(queue, [2]int{0, 0})
        seen[0] = true
        for len(queue) > 0 {
            cur := queue[0]
            x, y := cur[0], cur[1]
            queue = queue[1:]
            for _, dir := range dirs {
                nx, ny := x+dir[0], y+dir[1]
                for 0 <= nx && nx < h && 0 <= ny && ny < w && !seen[nx*w+ny] &&
                    abs(heights[x][y]-heights[nx][ny]) <= mid {
                    seen[nx*w+ny] = true
                    queue = append(queue, [2]int{nx, ny})
                }
            }
        }
        if seen[h*w-1] {
            right = mid
        } else {
            left = mid + 1
        }
    }
    return right
}

方法二：并查集

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66


type UnionFind struct {
    parent []int
}

func NewUnionFind(n int) *UnionFind {
    uf := &UnionFind{parent: make([]int, n)}
    for i := 0; i < n; i++ {
        uf.parent[i] = i
    }
    return uf
}

func (uf *UnionFind) Find(i int) int {
    if uf.parent[i] != i {
        uf.parent[i] = uf.Find(uf.parent[i])
    }
    return uf.parent[i]
}

func (uf *UnionFind) Union(i, j int) bool {
    n := len(uf.parent)
    iF, jF := uf.Find(i), uf.Find(j)
    uf.parent[iF] = jF
    if uf.Find(0)== uf.Find(n-1) {
        return true
    }
    return false
}

func abs(num int) int {
    if num < 0 {
        return -num
    }
    return num
}

func minimumEffortPath(heights [][]int) int {
    h, w := len(heights), len(heights[0])
    if h == 1 && w == 1 {
        return 0
    }
    var edges [][3]int
    for i := 0; i < h; i++ {
        for j := 0; j < w; j++ {
            if i > 0 {
                edges = append(edges, [3]int{(i-1)*w + j, i*w + j,
                    abs(heights[i-1][j] - heights[i][j])})
            }
            if j > 0 {
                edges = append(edges, [3]int{i*w + j - 1, i*w + j,
                    abs(heights[i][j-1] - heights[i][j])})
            }
        }
    }
    sort.Slice(edges, func(i, j int) bool {
        return edges[i][2] < edges[j][2]
    })
    uf := NewUnionFind(h * w)
    for _, edge := range edges {
        u, v := edge[0], edge[1]
        if uf.Union(u, v) {
            return edge[2]
        }
    }
    return -1
}