1659. 最大化网格幸福感

题目描述

给你四个整数 m、n、introvertsCount 和 extrovertsCount 。有一个 m x n 网格，和两种类型的人：内向的人和外向的人。总共有 introvertsCount 个内向的人和 extrovertsCount 个外向的人。

请你决定网格中应当居住多少人，并为每个人分配一个网格单元。 注意，不必 让所有人都生活在网格中。

每个人的 幸福感 计算如下：

• 内向的人 开始 时有 120 个幸福感，但每存在一个邻居（内向的或外向的）他都会 失去  30 个幸福感。
• 外向的人 开始 时有 40 个幸福感，每存在一个邻居（内向的或外向的）他都会 得到  20 个幸福感。

邻居是指居住在一个人所在单元的上、下、左、右四个直接相邻的单元中的其他人。

网格幸福感 是每个人幸福感的 总和 。 返回 最大可能的网格幸福感 。

示例 1：

• 输入：m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
• 输出：240
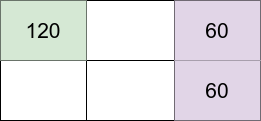
• 解释：假设网格坐标 (row, column) 从 1 开始编号。将内向的人放置在单元 (1,1) ，将外向的人放置在单元 (1,3) 和 (2,3) 。
  • 位于 (1,1) 的内向的人的幸福感：120（初始幸福感）- (0 * 30)（0 位邻居）= 120
  • 位于 (1,3) 的外向的人的幸福感：40（初始幸福感）+ (1 * 20)（1 位邻居）= 60
  • 位于 (2,3) 的外向的人的幸福感：40（初始幸福感）+ (1 * 20)（1 位邻居）= 60
  • 网格幸福感为：120 + 60 + 60 = 240

上图展示该示例对应网格中每个人的幸福感。内向的人在浅绿色单元中，而外向的人在浅紫色单元中。

示例 2：

• 输入：m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
• 输出：260
• 解释：将内向的人放置在单元 (1,1) 和 (3,1) ，将外向的人放置在单元 (2,1) 。
  • 位于 (1,1) 的内向的人的幸福感：120（初始幸福感）- (1 * 30)（1 位邻居）= 90
  • 位于 (2,1) 的外向的人的幸福感：40（初始幸福感）+ (2 * 20)（2 位邻居）= 80
  • 位于 (3,1) 的内向的人的幸福感：120（初始幸福感）- (1 * 30)（1 位邻居）= 90
  • 网格幸福感为： 90 + 80 + 90 = 260

示例 3：

• 输入：m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
• 输出：240

提示：

• 1 <= m, n <= 5
• 0 <= introvertsCount, extrovertsCount <= min(m * n, 6)

解法一：