1761. 一个图中连通三元组的最小度数

题目描述

给你一个无向图，整数 n 表示图中节点的数目，edges 数组表示图中的边，其中 edges[i] = [u_i, v_i] ，表示 u_i 和 v_i 之间有一条无向边。

一个 连通三元组 指的是三个节点组成的集合且这三个点之间两两有边。

连通三元组的度数 是所有满足此条件的边的数目：一个顶点在这个三元组内，而另一个顶点不在这个三元组内。

请你返回所有连通三元组中度数的 最小值 ，如果图中没有连通三元组，那么返回 -1 。

示例 1：

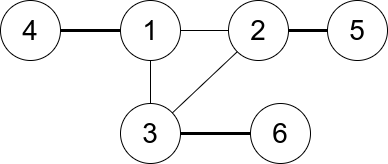
输入：n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
输出：3
解释：只有一个三元组 [1,2,3] 。构成度数的边在上图中已被加粗。

示例 2：

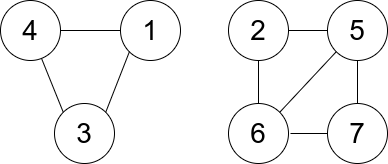
输入：n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
输出：0
解释：有 3 个三元组：
- 1. [1,4,3]，度数为 0 。
- 1. [2,5,6]，度数为 2 。
- 1. [5,6,7]，度数为 2 。

提示：

2 <= n <= 400
edges[i].length == 2
1 <= edges.length <= n * (n-1) / 2
1 <= u_i, v_i <= n
u_i != v_i
图中没有重复的边。

解法一：枚举每一个三元组

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


func min(nums ...int) int {
    res := nums[0]
    for _, num := range nums {
        if num < res {
            res = num
        }
    }
    return res
}

func minTrioDegree(n int, edges [][]int) int {
    g, degree := make([][]bool, n), make([]int, n)
    for i := 0; i < n; i++ {
        g[i] = make([]bool, n)
    }
    for _, edge := range edges {
        u, v := edge[0]-1, edge[1]-1
        g[u][v], g[v][u] = true, true
        degree[u]++
        degree[v]++
    }
    ans := math.MaxInt32
    for i := 0; i < n; i++ {
        for j := i + 1; j < n; j++ {
            if g[i][j] {
                for k := j + 1; k < n; k++ {
                    if g[i][k] && g[j][k] {
                        ans = min(ans, degree[i]+degree[j]+degree[k]-6)
                    }
                }
            }
        }
    }
    if ans == math.MaxInt32 {
        return -1
    } else {
        return ans
    }
}