1782. 统计点对的数目

题目描述

给你一个无向图，无向图由整数 n ，表示图中节点的数目，和 edges 组成，其中 edges[i] = [u_i, v_i] 表示 u_i 和 v_i 之间有一条无向边。同时给你一个代表查询的整数数组 queries 。

第 j 个查询的答案是满足如下条件的点对 (a, b) 的数目：

a < b
cnt 是与 a 或者 b 相连的边的数目，且 cnt 严格大于 queries[j] 。

请你返回一个数组 answers ，其中 answers.length == queries.length 且 answers[j] 是第 j 个查询的答案。

请注意，图中可能会有 重复边 。

示例 1：

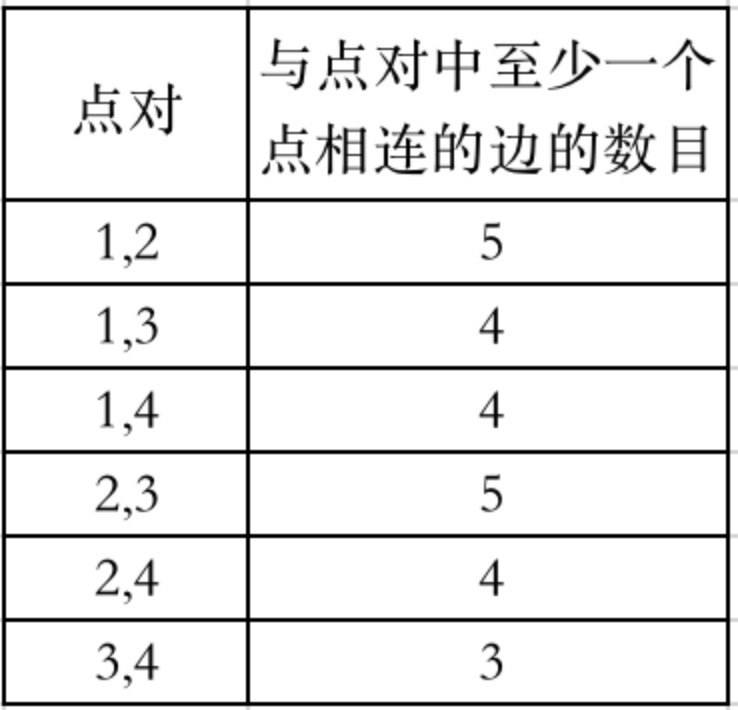
输入：n = 4, edges = [[1,2],[2,4],[1,3],[2,3],[2,1]], queries = [2,3]
输出：[6,5]
解释：每个点对中，与至少一个点相连的边的数目如上图所示。

示例 2：

输入：n = 5, edges = [[1,5],[1,5],[3,4],[2,5],[1,3],[5,1],[2,3],[2,5]], queries = [1,2,3,4,5]
输出：[10,10,9,8,6]

提示：

2 <= n <= 2 * 10⁴
1 <= edges.length <= 10⁵
1 <= u_i, v_i <= n
u_i != v_i
1 <= queries.length <= 20
0 <= queries[j] < edges.length

解法一：二分查找

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43


func max(nums ...int) int {
    res := nums[0]
    for _, num := range nums {
        if num > res {
            res = num
        }
    }
    return res
}

func countPairs(n int, edges [][]int, queries []int) []int {
    degree := make([]int, n)
    cnt := make(map[int]int)
    for _, edge := range edges {
        u, v := edge[0]-1, edge[1]-1
        if u > v {
            u, v = v, u
        }
        degree[u]++
        degree[v]++
        cnt[u*n+v]++
    }

    arr := make([]int, n)
    copy(arr, degree)
    sort.Ints(arr)
    var ans []int
    for _, bound := range queries {
        total := 0
        for i := 0; i < n; i++ {
            j := sort.SearchInts(arr, bound-arr[i]+1)
            total += n - max(i+1, j)
        }
        for val, freq := range cnt {
            u, v := val/n, val%n
            if degree[u]+degree[v] > bound && degree[u]+degree[v]-freq <= bound {
                total--
            }
        }
        ans = append(ans, total)
    }
    return ans
}