2352. 相等行列对

题目描述

给你一个下标从 0 开始、大小为 n x n 的整数矩阵 grid ，返回满足 R_i 行和 C_j 列相等的行列对 (R_i, C_j) 的数目。

如果行和列以相同的顺序包含相同的元素（即相等的数组），则认为二者是相等的。

示例 1：

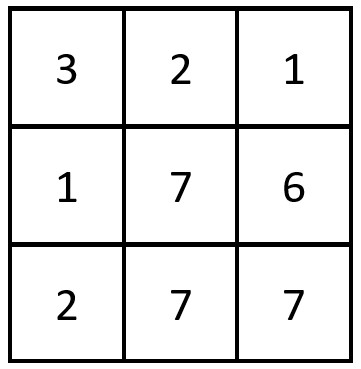
输入：grid = [[3,2,1],[1,7,6],[2,7,7]]
输出：1
解释：存在一对相等行列对： (第 2 行，第 1 列)：[2,7,7]

示例 2：

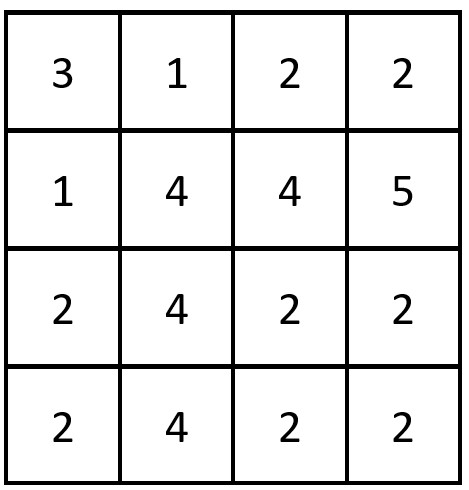
输入：grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
输出：3
解释：存在三对相等行列对：
- (第 0 行，第 0 列)：[3,1,2,2]
- (第 2 行, 第 2 列)：[2,4,2,2]
- (第 3 行, 第 2 列)：[2,4,2,2]

提示：

n == grid.length == grid[i].length
1 <= n <= 200
1 <= grid[i][j] <= 10⁵

解法一：暴力枚举

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


func equalPairs(grid [][]int) int {
    n := len(grid)
    res := 0
    for rowIdx := 0; rowIdx < n; rowIdx++ {
        for colIdx := 0; colIdx < n; colIdx++ {
            flag := true
            for i := 0; i < n; i++ {
                if grid[rowIdx][i] != grid[i][colIdx] {
                    flag = false
                    break
                }
            }
            if flag {
                res++
            }
        }
    }
    return res
}

解法二：哈希表

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


func equalPairs(grid [][]int) int {
    n := len(grid)
    record := make(map[string]int)
    for _, row := range grid {
        record[fmt.Sprint(row)]++
    }
    res := 0
    for j := 0; j < n; j ++ {
        tmp := make([]int, n)
        for i := 0; i < n; i++ {
            tmp[i] = grid[i][j]
        }
        if cnt, has := record[fmt.Sprint(tmp)]; has {
            res += cnt
        }
    }
    return res
}