2699. 修改图中的边权

题目描述

n 个节点的 无向带权连通 图，节点编号为 0 到 n - 1 ，再给你一个整数数组 edges ，其中 edges[i] = [a_i, b_i, w_i] 表示节点 a_i 和 b_i 之间有一条边权为 w_i 的边。

部分边的边权为 -1（w_i = -1），其他边的边权都为正数（w_i > 0）。

你需要将所有边权为 -1 的边都修改为范围 [1, 2 * 10⁹] 中的 正整数 ，使得从节点 source 到节点 destination 的 最短距离 为整数 target 。如果有多种修改方案可以使 source 和 destination 之间的最短距离等于 target ，你可以返回任意一种方案。

如果存在使 source 到 destination 最短距离为 target 的方案，请你按任意顺序返回包含所有边的数组（包括未修改边权的边）。如果不存在这样的方案，请你返回一个 空数组 。

注意: 你不能修改一开始边权为正数的边。

示例 1：

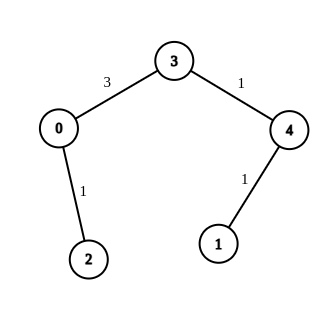
输入：n = 5, edges = [[4,1,-1],[2,0,-1],[0,3,-1],[4,3,-1]], source = 0, destination = 1, target = 5
输出：[[4,1,1],[2,0,1],[0,3,3],[4,3,1]]
解释：上图展示了一个满足题意的修改方案，从 0 到 1 的最短距离为 5 。

示例 2：

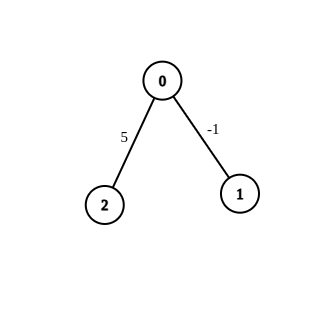
输入：n = 3, edges = [[0,1,-1],[0,2,5]], source = 0, destination = 2, target = 6
输出：[]
解释：上图是一开始的图。没有办法通过修改边权为 -1 的边，使得 0 到 2 的最短距离等于 6 ，所以返回一个空数组。

示例 3：

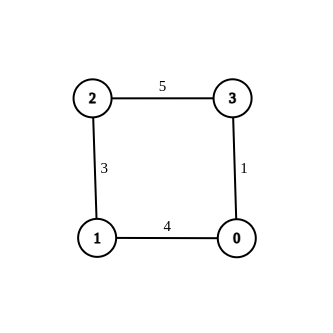
输入：n = 4, edges = [[1,0,4],[1,2,3],[2,3,5],[0,3,-1]], source = 0, destination = 2, target = 6
输出：[[1,0,4],[1,2,3],[2,3,5],[0,3,1]]
解释：上图展示了一个满足题意的修改方案，从 0 到 2 的最短距离为 6 。

提示：

1 <= n <= 100
1 <= edges.length <= n * (n - 1) / 2
edges[i].length == 3
0 <= a_i, b_i < n
w_i = -1 或者 1 <= w_i <= 10⁷
a_i != b_i
0 <= source, destination < n
source != destination
1 <= target <= 10⁹
输入的图是连通图，且没有自环和重边。

解法一：Dijkstra 算法 + 二分查找

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93


func modifiedGraphEdges(n int, edges [][]int, source int, destination int, target int) [][]int {
    var cnt int64
    for _, e := range edges {
        if e[2] == -1 {
            cnt++
        }
    }

    adjMatrix := make([][]int, n)
    for i := 0; i < n; i++ {
        adjMatrix[i] = make([]int, n)
    }
    diff := int64(target - 1)
    constructMatrix := func(idx int64) {
        for i := 0; i < n; i++ {
            for j := 0; j < n; j++ {
                adjMatrix[i][j] = -1
            }
        }
        for _, e := range edges {
            u, v, weight := e[0], e[1], e[2]
            if weight == -1 {
                if idx >= diff {
                    weight = target
                    idx -= diff
                } else {
                    weight = int(1 + idx)
                    idx = 0
                }
            }
            adjMatrix[u][v], adjMatrix[v][u] = weight, weight
        }
    }

    dijkstra := func() int {
        dst := make([]int, n)
        for i := 0; i < n; i++ {
            dst[i] = math.MaxInt32
        }
        used := make([]bool, n)
        dst[source] = 0
        for round := 0; round < n-1; round++ {
            u := -1
            for i := 0; i < n; i++ {
                if !used[i] && (u == -1 || dst[i] < dst[u]) {
                    u = i
                }
            }
            used[u] = true
            for i := 0; i < n; i++ {
                if !used[i] && (adjMatrix[u][i] != -1 && dst[i] > adjMatrix[u][i]+dst[u]) {
                    dst[i] = adjMatrix[u][i] + dst[u]
                }
            }
        }
        return dst[destination]
    }

    constructMatrix(0)
    if dijkstra() > target {
        return nil
    }
    constructMatrix(cnt * diff)
    if dijkstra() < target {
        return nil
    }

    var left, ans int64
    right := cnt * diff
    for left <= right {
        mid := left + (right-left)/2
        constructMatrix(mid)
        if dijkstra() >= target {
            ans = mid
            right = mid - 1
        } else {
            left = mid + 1
        }
    }

    for _, e := range edges {
        if e[2] == -1 {
            if ans >= diff {
                e[2] = target
                ans -= diff
            } else {
                e[2] = 1 + int(ans)
                ans = 0
            }
        }
    }
    return edges
}